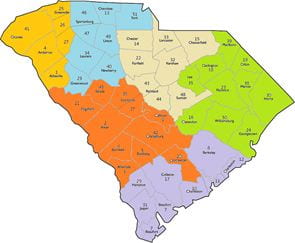
In a competitive district such as this illustration from the paper, the maximum support advantage of either party is at most 10%. These parameters can be selected by the redistributing commissions, including the number of competitive districts and the vote split.
The unfair and non-competitive political redistricting process known as gerrymandering could be solved using new mathematical models and computer implementation, according to a recent study by a San Jose State University research team that appeared in Computers & Industrial Engineering, an Elsevier publication.*
“Election and redistricting are political processes; we believe that software tools are needed to achieve political purposes,” said one of the paper’s authors, Dr. Jacob Tsao, a professor of Industrial Systems Engineering. “We present two mathematical optimization models to implement political fairness and competitiveness.” Both models are implemented with a case study of South Carolina.
There appears to be a growing movement against gerrymandering. In December 2019 a New York Times columnist observed that State courts in Pennsylvania and Virginia have thrown out gerrymandered maps, voters in Arizona, California and Michigan approved ballot measures to reduce gerrymandering, and similar measures could be on the ballot in 2020 in Arkansas and Oregon.
“Redistricting can be formulated and solved as a difficult purely mathematical problem, without any partisan biases; such efforts started as early as the 1960s but continued intermittently and sparsely,” wrote the San Jose State team in their study, hoping that their research will assist redistricting commissions and their staff members by developing a suite of mathematical models and their computer implementations to develop and optimize districting plans.
“Hopefully, this is a timely paper for the political redistricting work to occur across the United States in response to the ongoing 2020 US Census and in preparation for the 2022 election and beyond,” said Tsao. The team writing the paper included not only SJSU faculty and students but alumni as well. “The first author of this paper, Dr. Hongrui Liu, was an MS-Industrial & Systems Engineering (ISE) student about 15 years ago,” explained Tsao. “She and I published a journal paper in 2008 on the design of experiments, with an unconventional approach, based on her MS Project. She went on to earn a Ph.D. from the University of Washington in 2010. After working for several years in the energy industry, she joined SJSU ISE faculty in 2017.”
San Jose State’s math department is also thinking about politics, offering Math 10P (Mathematics in Politics) for the first time in spring 2020. The course description states: “Did you know that there’s a state in the U.S. where one party gets 52% of the vote, but nevertheless holds 75% of that state’s seats in Congress? Did you know that San Francisco, Oakland, Berkeley, San Leandro, and the state of Maine use a different system for counting votes than most of the rest of America?
“Believe it or not, the key to understanding all of that and more is math! In Math 10P, Mathematics in Politics, you’ll learn not only the mathematical secrets behind all of those phenomena, but also how, through politics, math impacts our daily lives and the future of America. Recommended for anyone with an interest in politics, current events, or in how math and politics affects our daily lives. Fulfills [the] Math/Quantitative Reasoning requirement.”
*“Mathematical models of political districting for more representative governments” by Hongrui Liu, Ayca Erdogan, Royce Lin (a SJSU MS-Industrial & Systems Engineering Student), and H.-S. Jacob Tsao. Computers & Industrial Engineering, an Elsevier publication. Volume 140, February 2020, 106265.